Eléments de géométrie⚓
Quelques citations pour commencer...
« Ce qui est affirmé sans preuve peut être nié sans preuve »
- Euclide (Environ 300 av J.C.) - Mathématicien
« L'aveugle est le mieux placé pour faire de la géométrie. »
- René Descartes (1596 - 1650) - Mathématicien, physicien, philosophe 
Définition : Figure de géométrie
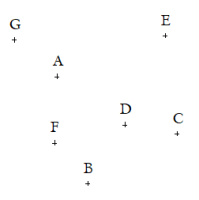
Une figure de géométrie plane est formée d'un ensemble (fini ou infini) de points.
Un point est représenté par une croix et est nommé en utilisant une lettre majuscule marquée à proximité du point.
Attention :
Dans une même figure de géométrie, deux points distincts ne portent jamais le même nom. On n'utilise donc que des lettres différentes pour nommer les différents points.
Définition : La droite
Une droite est constituée d'une infinité de points alignés et elle est illimitée des deux côtés.
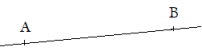
La droite qui passe par les points A et B se prolonge indéfiniment du côté du point A et du côté du point B.
La droite qui passe par les points A et B se note (AB) ou (BA).
Définition : Le segment
Un segment est une portion de droite située entre deux points, appelés extrémités.
Un segment est donc constitué d'une infinité de points alignés, il est limité des deux côtés par ses extrémités et ne peut donc pas être prolongé.
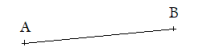
Le segment qui a pour extrémités les points A et B se note [AB] ou [BA].
Définition : La demi-droite
Une demi-droite est la partie d'une droite située d'un côté d'un point placé sur cette droite, appelé origine.
Une demi-droite est donc constituée d'un infinité de points alignés, elle est limitée d'un côté par son origine et peut donc être prolongée d'un seul côté.
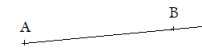
La demi-droite qui a pour origine A et qui passe par B se prolonge indéfiniment du côté du point B.
La demi-droite d'origine A passant par B se note [AB).
Attention : Notation d'une demi-droite
Dans la notation d'une demi-droite, on cite toujours l'origine en premier afin de ne pas confondre les deux tracés possibles :
La demi-droite d'origine A passant par B, notée [AB) :
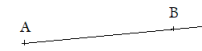
La demi-droite d'origine B passant par A notée [BA) :
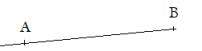
Définition : Intersection
Lorsque deux objets géométriques ont au moins un point en commun, on dit qu'ils sont sécants et on appelle les points communs des points d'intersection.
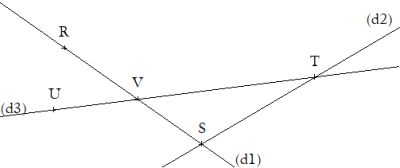
V est le point d'intersection des droites (d1) et (d3).
Le point d'intersection des droites (d1) et (d2) est S.
Les droites (d2) et (d3) sont sécantes en T.
Définition : Appartenance
On dit qu'un point appartient à un objet géométrique s'il fait partie des points qui constituent cet objet.
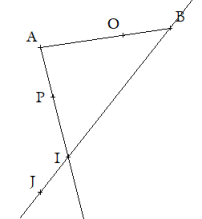
Le point O appartient au segment [AB].
Le point P appartient à la demi-droite [AI).
Le point J appartient à la droite (BI).
Le point P appartient au segment [AI].
Le point J n'appartient pas au segment [BI].
Le point P n'appartient pas à la droite (BI).
Pour dire qu'un point appartient à un ensemble donné, on utilise le symbole 
.
Pour dire qu'un point n'appartient pas à un ensemble donné, on utilise le symbole 
.
O [AB]
P [AI)
J (BI)
P [AI]
J [BI]
P (BI)